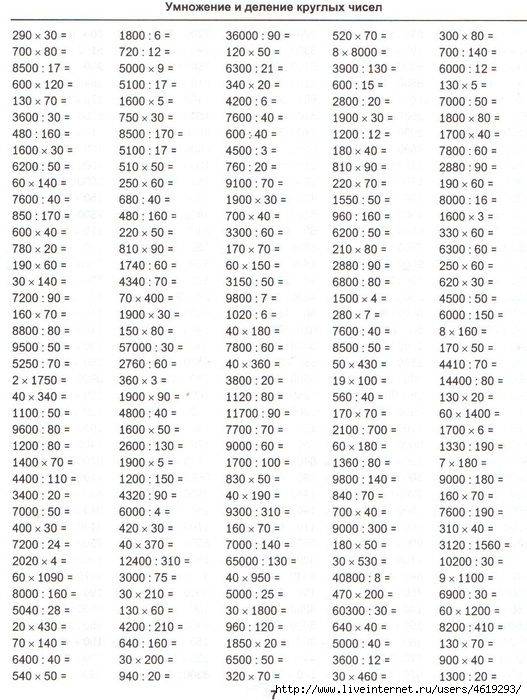
Задачи, решаемые геометрическим способом
Пример 1
В доме 4 двери. Ширина каждой 1 метр, высота — 2 метра. Сколько нужно белил, чтобы покрасить их с обеих сторон, при условии, что на 1 квадратный метр поверхности требуется 100 грамм белил? Ответ дайте в граммах.
Решение
- Для решения нужно вычислить площадь каждой двери, которую нужно покрасить. Для этого используем формулу площади прямоугольника – S=ab, где a и b – длины сторон. Подставляем числа из условия и получаем: S=2×1=2 м2;
- Далее умножаем площадь на 2, потому что каждую дверь нужно окрасить с двух сторон. Получаем 2×2=4 м2. То есть, покрасочная площадь каждой двери равна 4 квадратным метрам;
- Посчитаем общую площадь для всех дверей. Для этого умножаем площадь одной на их количество: 4×4=16 м2;
- Главный вопрос задачи — сколько потребуется белил для всех дверей? Чтобы посчитать умножаем количество, требующееся на 1 квадратный метр на всю площадь: 100×16=1600 грамм;
- Записываем это значение в ответ.
Пример 2
Площадь прямоугольника 192 квадратных сантиметра, длина одной из сторон — 16 см. Найдите периметр прямоугольника.
Решение
- Для начала нужно посчитать другую сторону прямоугольника. Делается это с помощью формулы площади: S=ab, где a и b — длины сторон. Подставляем числа и получаем: 192=16*a. Отсюда получается, что вторая сторона — 12 см;
- Для нахождения периметра воспользуемся формулой P=2(a+b). Подставляем числа и получаем: P=2(16+12)=2×28=56 см;
- Найденное значение записываем в ответ.
Для решения геометрических задач нужно знать наизусть все формулы площадей и периметров. Без этого не получится даже приступить к решению задания.
§ 3адания на тему «Квадрат и куб числа»

Во время изучения математики в школе ученикам часто задаются задания на вычисление квадратов и кубов чисел. Это помогает им закрепить знания о свойствах чисел и развить навыки аналитического мышления.
Например, учитель может предложить ученикам задачу по определению количества ящиков, необходимых для упаковки определенного количества грибов. Если известно, что в одном ящике помещается 25 грибов, а всего нужно упаковать 125 грибов, то ученики могут воспользоваться знанием о свойствах кубов чисел и вычислить, что нужно 5 ящиков.
Другим примером задачи на вычисление квадрата числа может быть задание по определению длины пути, который преодолел пешеход. Если известно, что путь, который он прошел, был равен 9 километрам, то можно найти квадрат числа 9 и получить ответ — 81, что будет являться длиной пути в квадратных километрах.
Также ученикам могут предлагаться задачи на составление выражений или нахождение длины отрезка. Например, задача может состоять в том, чтобы найти длину отрезка между двумя точками на числовой оси, зная координаты этих точек. Для решения такой задачи ученикам нужно воспользоваться формулой для нахождения расстояния между двумя точками на числовой оси, которая называется формулой модуля разности.
Почему важно уметь решать задачи по математике
Математика — точная дисциплина, связанная с вычислениями. Но её часто называют царицей всех наук. Это не просто так. Основное, чему учатся дети — решение конкретно поставленных задач
Это самое важное для развития любого человека
Для построения правильного ответа на задачу нужно выделить:
- главную мысль;
- заданное условие;
- что требуется найти;
- связь между искомым и данным.

Математика — один из самых важных предметов в школьной программе
На основе этого строится логичное решение с использованием условий для получения требуемого результата. Вместе с этим развивается познавательная активность, логические мышление.
Задачи, решаемые алгебраическим способом
Пример 1
Из цистерны отлили 80 литров молока, в нем осталось на 240 литров больше, чем отлили. Сколько литров молока было в цистерне с самого начала?
Решение
- Начинаем с составления краткого условия в виде таблицы. В подобных типовых задачах нужно обозначать неизвестное за «x»;
- Потребуются три строки: сколько молока было, сколько его отлили и сколько осталось;
- Заполняем числами таблицу;
Таблица 7 — краткое условие задачи
| Было | Х |
|---|---|
| Отлили | 80 |
| Осталось | 240+80 |
- Приступаем к расчётам. Нам нужно узнать, сколько было молока изначально. Для этого составляем уравнение. От начального количества вычитаем отлитое и получаем остаток;
- Математически получаем такую запись: x-80=240+80;
- Начинаем решение с того, что считаем всё, что можно посчитать. В данном случае складываем правую часть уравнения. 240+80=320. Теперь уравнение имеет вид: x-80=320;
- Теперь находим «x». Используем базовое правило математики и получаем следующее: x=320+80. Считаем правую часть и получаем: x=400;
- Возвращаемся к началу и смотрим, что мы обозначили за «x». В этом примере за икс мы взяли объём молока, который был изначально. То есть, изначально было 400 литров молока;
- Записываем полученное значение в ответ.
Пример 2
Первое слагаемое на 52 больше второго слагаемого, а второе слагаемое на 14 меньше третьего слагаемого. Сумма трех слагаемых равна 327. Найдите каждое слагаемое.
- Записываем краткое условие в виде таблицы;
- Потребуется четыре строки, так как нам дали три слагаемых и их сумму;
- Заполняем таблицу числами, обозначив за икс последнее слагаемое. Выбираем третье, потому что от него зависят все остальные;
Таблица 8 — краткое условие задачи
| 1 слагаемое | (x-14)+52 |
|---|---|
| 2 слагаемое | x-14 |
| 3 слагаемое | x |
| Сумма | 327 |
- Приступаем к расчётам. Для нахождения слагаемых нужно решить уравнение, после чего число подставить в выражения из таблицы.
- Уравнение составляется исходя из условия – три слагаемых и сумма – складываем значения из второго столбца таблицы и приравниваем это к сумме.
- Получится такое выражение: (x-14)+52+(x-14)+x=327.
- Открываем скобки и упрощаем выражение: 3x+24=327.
- Переносим числа в правую часть: 3x=303
- Считаем икс: 303:3=101.
- Теперь подставляем число 101 в таблицу вместо икса.
- Получается третье слагаемое равно 101; второе: 101-14=87; первое: 87+52=139.
- Эти числа записываем в ответ. Легко проверить правильность решения просто сложив эти значения. Если пример получается правильный, то и решено всё верно.
Для правильного решения этих типовых задач необходимо ничего не напутать с иксом. Лучше потратить больше времени и сразу всё проверить, чем переделывать задание сначала. Неправильное обозначение повлечёт за собой ошибку на протяжении всего решения
Математика, 5 класс – Математическая эстафета в 5 классе
Публикация «Математическая эстафета в 5…»
Цель мероприятия: обучающие: расширить понятия базового уровня; научить решать нестандартные задачи; развивающие: развитие познавательного интереса, математической интуиции, логического мышления, внимания, памяти, творческой деятельности учащихся, математического языка;…
Библиотека изображений «МААМ-картинки»
Задачи на формирование математической и финансовой грамотности в образовательной деятельности (5–9 классы)
Задачи можно использовать на уроках и во внеурочное время: 1. Реши примеры, составь из ответов пятизначное число и ты узнаешь, сколько человек проживает в Приморско-Ахтарском районе по данным 2022 года: 1) -18 : – 6) 2) 24,4 : 6,1 3) 0,366 : 0,061 4) 100,2 : 20,04 5) 54,3 – 53,3…
Рабочая программа учебного предмета «Математика» для 5 класса
ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА “МАТЕМАТИКА” Рабочая программа по математике для обучающихся 5 классов разработана на основе Федерального государственного образовательного стандарта основного общего образования с учётом и современных мировых требований, предъявляемых к…
Разработка урока по математике с использованием цифровых образовательных ресурсов в 5 классе
Предмет: математика Класс: 5 Тема: Объем прямоугольного параллелепипеда Текст задания: Сколько мусора производит семья за один месяц? Цифровой ресурс: интернет-ресурсы: образовательная платформа Учи.ру – https://uchi.ru , Открытая школа 2035- https://2035school.ru Возможный…
Контрольные работы с ответами. 5 класс
УМК МЕРЗЛЯК: Дидактические материалы: Контрольные работы (10 КР)УМК МЕРЗЛЯК: Дидактические материалы: Самостоятельные работы (34 СР)УМК МЕРЗЛЯК: Буцко. Методическое пособие для 5 класса (10 КР)УМК МЕРЗЛЯК: Ерина. Тесты в 5 классе к новому учебнику (7 тестов)
УМК ВИЛЕНКИН: Попова. Контрольно измерительные материалы (14 КР)УМК ВИЛЕНКИН: Жохов и др. Контрольные работы по математике 5 кл (15 КР)УМК ВИЛЕНКИН: Глазков. Контрольно-измерительные материалы в 5 классе (14 КР)УМК ВИЛЕНКИН: Попов. Дидактические материалы: Контрольные (14 КР)
УМК НИКОЛЬСКИЙ: Потапов, Дидактические материалы — Контрольные (9 КР)УМК НИКОЛЬСКИЙ: Ерина. Контрольные работы по математике (9 КР)
УМК — ДОРОФЕЕВ: Кузнецова и др. Математика Контрольные работы (7 КР)
К любому УМК — Ершова. Самостоятельные и контрольные работы для 5 класса (15 КР)
Регулярное выполнение работ с тестами и контрольных работ поможет учителям и учащимся своевременно получать информацию о полноте усвоения учебного материала. Тематические тесты могут быть включены в урок на любом этапе: актуализации знаний, закрепления изученного, повторения. Онлайн форма тестирования внесет разнообразие в контроль и коррекцию знаний, умений и навыков, не отнимут много времени у учителя. В то же время анализ выполнения тестов поможет выделить повторяющиеся ошибки как индивидуально у каждого ученика, так и в целом по классу.
Учебные пособия для очного контроля знаний
по математике в 5 классе
Дидактические материалы по математике. 5 класс. К учебнику Виленкина Н.Я. и др. — Попов М.А. (2017 -112с.)
Контрольные и самостоятельные работы по математике. 5 класс. К учебнику Виленкина Н.Я. и др. Попов М.А. (2016, 96с.)
Математический тренажер. 5 класс. Жохов В.И. (2019, 80с.)
Математика 5 кл. Контрольные измерительные материалы. Глазков Ю.А., Ахременкова В.И., Гаиашвили М.Я. (2014, 96с.)
Математика. 5 класс. Контрольные работы. Жохов В.И., Крайнева Л.Б. (2012, 64с.)
Математика. 5 класс. Контрольные работы в новом формате. Александрова В.Л. (2011, 96с.)
Математика. 5 класс. Тестовые материалы для оценки качества обучения. Гусева И.Л. (2011, 88с.)
Самостоятельные и контрольные работы по математике. 5 класс. Смирнова Е.С. (2004, 160с.)
Математика. 5 класс. Тематические тесты. Кузнецова Л.В., Минаева С.С., Рослова Л.О. (2017, 112с.)
Математика. 5 класс. Дидактические материалы. Кузнецова Л.В., Минаева С.С. и др. (2014, 128с.)
Математика. Дидактические материалы. 5 класс. Дорофеев Г.В., Кузнецова Л.В. и др. (2010, 110с.)
Тесты по математике. 5 класс. К учебнику Зубаревой И.И., Мордковича А.Г. — Рудницкая В.Н. (2013, 128с.)
Дидактические материалы по математике. 5 класс, к учебнику Зубаревой И.И., Мордковича А.Г. — Рудницкая В.Н. (2017, 160с.)
Математика. 5-6 классы. Тесты. Тульчинская Е.Е. (2014, 96с.)
Математика 5. Промежуточное тестирование. Ключникова Е.М., Комиссарова И.В. (2014, 80с.)
Тесты по математике. 5 класс. К учебнику А.Г. Мерзляка и др. — Ерина Т.М. (2017, 96с.)Математика. 5 класс. Дидактические материалы. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. (2017, 144с.)
Тесты по математике. 5 класс. К учебнику Никольского С.М. и др. — Журавлев С.Г., Ермаков В.В. и др. (2013, 128с.)
Математика. 5 класс. Дидактические материалы. Потапов М.К., Шевкин А.В. (2017, 96с.)
Как решить проблемы с математикой
Как только у ребёнка появляются проблемы с математикой родители почему-то начинают думать, что причина заключается в плохой предрасположенности к точным наукам. Потому что формулы вроде бы знает, простые примеры решить тоже может, но каждая контрольная и самостоятельная работа превращается в целое испытание для всей семьи. Все сидят в ожидании результатов. Никогда нельзя сказать точно какую оценку получит ребёнок — четвёрку или двойку.

Дети часто получают плохие отметки именно по математике
Также много жалоб по типу: занимаемся все выходные напролёт, учим эту математику, учим, а в итоге всё равно результат прежний. На самом деле, причина такого плохого восприятия — отсутствие адекватных причин заниматься всеми этими цифрами. Большинство родителей сходятся во мнении, что ребёнок просто гуманитарий, главное — литература, история, обществознание, а математика неважна.
Гуманитариям математика не нужна?
Это огромная ошибка, ведь для лучшего восприятия точных наук этому самому «гуманитарию» нужно лишь вдохновение и цель. Отлично будет, если ребёнку объяснить, что математика — это такая же наука, как и любая другая, и она не ограничивается уравнениями и задачами. Это нечто большее. Математика позволяет изменить мышление, воспринимать старые вещи по-новому.
Главная проблема всех гуманитариев, которые имели проблемы с математикой — это логика. Для составления, например, грамотной и структурированной статьи нужно руководствоваться не только правилами русского языка, но и логикой изложения мысли. Все части должны быть связаны между собой, в то же время, должны легко читаться отдельные фрагменты.
Именно логическое мышление в первую очередь развивает математика и воспринимать это нужно, как возможность расширения кругозора и свежего взгляда на старое. Также точные науки помогают дисциплинировать свой ум и комплексно подходить к решению поставленных задач.
Математика — сложный предмет
Самая популярная отговорка заключается в том, что математика — самый сложный предмет из всех. Нет, на самом деле это одна из самых простых и понятных дисциплин. Для сравнения, возьмите наш богатый русский язык.
Мало того, что в нём существует немало правил орфографии, пунктуации, стилистики, так ещё и исключения есть почти в каждом правиле. Вот уж где нужно запоминать «тонну» информации.
В то же время в математике существуют базовые правила, на которых строятся все остальные. То есть, более сложное всегда можно привести к простому. Всё построено на железной логике, и, следуя этим правилам, вы сможете решить задачи, которые казались на первый взгляд непосильными.
Вспомните, как учат всех детей. Для того, чтобы научить их писать, сначала нужно выводить палочки, точки, изгибы. Потом уже буквы, а из букв — простые слова, из слов — предложения.
Начните изучать математику с самых простых уравнений
В математике с самого начала всё объясняется на пальцах или предметах. При этом, за то же самое время, потраченное на русский язык и на математику, прогресс в изучении второй будет больше. Например, считать учатся дети на яблоках, конфетках.
Используйте это и для решения более сложных задач. В пятом классе аналогии привести не составит труда. Это поможет ребёнку ассоциировать вычисления не с сухими числами, а, например, с мандаринами.
§ Задания на тему «Сложение вычитания натуральных чисел»
Одной из основных операций в математике является сложение и вычитание натуральных чисел. Это важные навыки, которые необходимо освоить в начальной школе. В данном разделе представлены задания, которые помогут ученикам 5 класса закрепить данную тему.
Задания на сложение представлены в виде примеров, где необходимо найти сумму двух или более цифр. Например, задача может быть сформулирована следующим образом: «Толя купил в магазине 3 рулона ткани длиной 5 метров каждый. Сколько всего метров ткани купил Толя?». Чтобы решить эту задачу, необходимо сложить длины всех рулонов: 5 + 5 + 5 = 15. Ответом будет число 15 метров.
Задания на вычитание связаны с определением разности двух чисел. Например, рассмотрим задачу: «У Маши было 10 капуст, а она продала 5. Сколько капуст осталось у Маши?». В данном случае необходимо из общего количества капуст (10) вычесть количество проданных капуст (5). Разность будет составлять 5 капуст.
Иногда для решения задач по сложению и вычитанию необходимо использовать дробные числа. Например, задача может быть такой: «Между двумя садами расстояние составляет 2,5 км. Одной части пути между садами Лена прошла пешком, а остальную часть – на велосипеде. Пешком она прошла 1,2 км. Какое расстояние Лена проехала на велосипеде?». Чтобы решить данную задачу, необходимо от общего расстояния (2,5 км) отнять пройденное пешком (1,2 км). Ответом будет число 1,3 км.
Также в заданиях на сложение и вычитание могут использоваться большие числа, например, тысячи и сотни. Например, задача может быть сформулирована следующим образом: «Мама сделала 8 пирогов. Для каждого пирога было использовано 3 яблока. Сколько всего яблок было использовано для пирогов?». Чтобы решить эту задачу, необходимо умножить количество пирогов (8) на количество яблок в каждом пироге (3): 8 * 3 = 24. Ответом будет число 24 яблока.
§ Задания для 5 класса на тему «Натуральные числа»

Одной из задач, которую решает 5 класс, является задача о сравнении натуральных чисел. Например, нужно определить, какое из двух чисел больше или меньше
Для решения таких задач важно знать правила сравнения чисел: если у числа больше разрядов, то оно больше; если все разряды равны, а последнее, самое правое, отличается, то больше число будет то, у которого это разряд больше
В другом задании ребенку предлагается составить число, которое будет в несколько раз больше или меньше данного. Например, если дано число 25, то нужно написать число, которое будет в два раза больше или в два раза меньше.
В одной задаче ребенку было известно, что мама заплатила за новый автомобиль сумму, которая составляет 6 500 000 рублей. Ребенок должен был сделать вывод, что известно ему наперёд.
Задача для самостоятельного решения: на огороде у Лены растут 12 кустов капусты и 8 штук грибов. На таком же огороде растут 20 кустов капусты. Сколько штук грибов растет на таком же огороде?
Одной из задач, которые ребенок решает во втором классе, являются задачи на умножение и деление с использованием таблицы умножения. Например, ребенку задается вопрос: сколько будет 8 умножить на 9. Чтобы найти ответ, нужно использовать таблицу умножения.
В одной задаче ребенку предлагается составить уравнение для нахождения неизвестного числа. Например, ребенку дают известное число, а нужно составить уравнение, в котором нужно найти неизвестное число.
Одной из задач, которые ребенок решает в пятом классе, являются задачи на десятичные дроби. Например, ребенку дают числа 3,75 и 5,6 и нужно определить, какое из них больше или меньше.
Другая задача предлагает ребенку найти количество деревьев на участке. Для решения этой задачи нужно знать, что количество деревьев на участке обозначается числом.
Задача для самостоятельного решения: Толя и его друг пошли в сад. Путь до сада составляет 2 километра. Они решили пройти пешком и разделить путь на две равные части. Сколько каждый из них должен пройти?
Другая задача предлагает ребенку определить длину ткани. Например, ребенку дают кусок ткани длиной 3 метра и нужно определить, на сколько частей нужно разделить его, чтобы каждая часть была длиной 0,6 метра.
Формула спокойствия
Часто плохие оценки становятся причиной ссор между родителями и детьми. Это категорически неправильно. Вместо того, чтобы высказывать ребёнку, что он «ленится», «не думает о будущем» да и в общем «туго соображает», следует отвести от неудачи или помочь исправиться с ней.
Но под помощью подразумевается не «вдалбливание» и «зубрёжка» неинтересных формул и правил. Следует возбудить интерес к теме, которая была плохо воспринята. Да и к тому же поставить правильную цель ребёнку. Не нужно говорить, что от оценок зависит его будущее
Вообще не зацикливайте внимание на оценках
По исследованиям российских психологов дети, которые хотели стать врачами, инженерами и просто хорошими людьми, быстро повышали свою успеваемость
А те ученики, которым с первого класса «вдалбливают» в голову знания, думали только о том, как не стать худшим в классе, и уделяли своим отметкам слишком большое внимание
Лучшим вариантом по-прежнему остаются занятия с репетитором. Он сохранит нервы, и вам, и ребёнку. Обеспечивая нужное количество времени на обучение и выбрав правильный подход, ученик станет показывать результаты лучше прежнего. Но, моментально отличником вашего ребёнка это не сделает.
Надеемся, что вы смогли найти решение задач, которое искали. Также для понимания темы рекомендуем посмотреть видео по этой теме от организаторов специальной математической школы федерального уровня «Аристотель».
8.5 Total Score
Решение задач по математике
Некоторые ученики, как пятых, так и других классов, часто сталкиваются с проблемами в изучении математики. В этом случае родителям не стоит впадать в панику. Следует уделить больше внимания детальному разбору примеров и задач. Если это не улучшит успеваемость, есть смысл обратиться за помощью к репетитору.
Простота
7
Доступность
9
ПЛЮСЫ
- Подробные инструкции помогут разобраться в решении задач и примеров
- Для изучения математики можно пользоваться решебниками
МИНУСЫ
Полученных знаний в школе не всегда достаточно для понимания предмета
|
§ Задания на тему «Обыкновенные дроби»
Во время занятий по математике в 5 классе детям необходимо изучать и понимать такую тему, как обыкновенные дроби. Обыкновенными дробями называются числа, представленные дробью, где числитель и знаменатель — целые числа. Для вашей домашней работы предлагается несколько заданий, которые помогут усвоить эту тему более глубоко и лучше понять ее применение в практике.
- Составить уравнение: Вы путешествуете на автомобиле. За третий час вы проехали 2/5 всего пути. Зная, что весь путь составляет 625 километров, найдите сколько километров вы проехали за 3 часа.
- Работа с рулоном: Второй рулон обоев имеет длину 120 метров. В первом рулоне обои были распределены по стенам комнаты, затем второй рулон использовали для дальнейшей отделки. Какая часть обоев осталась неиспользованной?
- Решение уравнений: В самолете находились 86 пассажиров. 2/3 пассажиров сели сначала в Казани, затем еще 1/4 из Москвы. Сколько пассажиров прилетело в пункт назначения отдельно из Казани и отдельно из Москвы?
- Вычисления с десятичными дробями: В ящиках лежит 3,75 кг грушевых. Для продажи их нужно разложить в пакеты по 0,5 кг. Сколько пакетов нужно сделать?
- Работа с отрезком: Ребенок загадал число на числовой прямой между двумя другими числами. Если одно число равно -5/6, а второе число равно 1/3, то какое число загадано ребенком?
Решения этих заданий помогут вам лучше понять применение обыкновенных дробей в различных ситуациях и расширить навыки работы с ними. Успехов в изучении темы обыкновенных дробей!
Примеры 5 класс по математике для тренировки с дробями
1
2
3
4
5
6
7
8
9
.
C
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>5</p> <p class=’znam’>4</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>7</p> <p class=’znam’>4</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>7</p> <p class=’znam’>4</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>7</p> <p class=’znam’>4</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>6</p> <p class=’znam’>3</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>6</p> <p class=’znam’>10</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>7</p> <p class=’znam’>1</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>7</p> <p class=’znam’>10</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>9</p> <p class=’znam’>2</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>9</p> <p class=’znam’>5</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>9</p> <p class=’znam’>5</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>1</p> <p class=’znam’>9</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>2</p> <p class=’znam’>4</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>8</p> <p class=’znam’>6</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>5</p> <p class=’znam’>5</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>1</p> <p class=’znam’>7</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>2</p> <p class=’znam’>2</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>7</p> <p class=’znam’>2</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
<table class=’print_table_book’>
<tr>
<td>
<p class=’chisl’>5</p> <p class=’znam’>1</p>
</td>
<td class=’drob_operator’> + </td>
<td>
<p class=’chisl’>10</p> <p class=’znam’>1</p>
</td>
<td class=’drob_operator’> = </td>
</tr>
</table>
Средний уровень
Задание 1
Запишите числа цифрами:
- 1. Восемьсот семьдесят миллионов девять;
- 2. Два миллиарда четыреста пятьдесят девять миллионов триста шестьдесят восемь тысяч пятьсот семьдесят девять;
- 3. Тридцать миллиардов четыре миллиона двадцать три;
- 4. Восемьсот миллиардов шесть;
- 5. 248 миллиарда 6 миллионов 18 тысяч сто;
- 6. 503 миллиарда 241 тысяча 64.
Решение
| 1) 87 000 009 | 2) 2 459 368 579 | 3) 30 004 000 023 | 4) 800 000 000 006 | 5) 248 006 018 100 | 6) 503 000 241 064 |
Задание 2
Запишите числа, как сумму разрядных слагаемых:
| 1) 349 | 2) 809 | 3) 2475 | 4) 3008 |
Решение
| 1) 349 = 300 + 40 + 9 | 2) 809 = 800 + 9 | 3) 2475 = 2000 + 400 + 70 + 5 | 4) 3008 = 3000 + 8 |
Задание 3
Расставьте знаки больше или меньше:
| 852 618 … 852 681 | 2 545 033 … 2 545 300 | 300 300 003 … 300 003 300 |
Решение
| 852 618 < 852 681 | 2 545 033 < 2 545 300 | 300 300 003 > 300 003 300 |
Задание 4
Запишите числа в порядке возрастания:
98362, 6395, 1103672, 492031, 10238, 2958, 300271, 300713, 490952, 192, 74.
Решение
74, 192, 2 958, 6 395, 10 238, 98 362, 300 271, 300 713, 490 952, 492 031, 1 103 672.
Запишите натуральные числа, которые меньше 82 и больше 74.
Решение
75, 76, 77, 78, 79, 80, 81.
Задание 6
Какое количество натуральных чисел расположено между числами:
| 1) 57 и 64; | 2) 238 и 261; | 3) 167 и 192; | 4) 342 и 409; |
Решение
| 1) 6; | 2) 21; | 3) 24; | 4) 66. |
Задание 7
Выполните сложение:
| 27 592 + 593 089 = | 59 003 + 12 903 = | 129 301 + 739 912 = |
| 60 018 + 224 983 = | 30 283 + 45 037 = | 884 916 + 294 001 = |
Решение
| 27 592 + 593 089 = 620 681 | 59 003 + 12 903 = 71 906 | 129 301 + 739 912 = 869 213 |
| 60 018 + 224 983 = 285 001 | 30 283 + 45 037 = 75 320 | 884 916 + 294 001 = 1 178 917 |
Задание 8
Вычислите:
| 18м 48см + 26м 39см = ; | 45т 390 кг + 21т 31кг = . |
Решение
| 18м 48см + 26м 39см = 44м 87 см; | 45т 390 кг + 21т 31кг = 66т 421кг. |
Задание 9
Выполните вычитание:
| 49 081 – 19 090 = | 18 928 – 18 098 = | 397 802 – 65 834 = |
| 72 305 – 50 923 = | 25 730 – 21 829 | 450 038 – 375 340 = |
Решение
| 49 081 – 19 090 = 29 991 | 18 928 – 18 098 = 830 | 397 802 – 65 834 = 331 968 |
| 72 305 – 50 923 = 21 382 | 25 730 – 21 829 = 3 901 | 450 038 – 375 340 = 74 698 |
Задание 10
Найдите значения выражений:
| 469 + 1 843 – 1 992 = | 4 578 – 2640 + 3 654 = |
| 9 029 – 6 230 – 1 389 = | 19 463 + 7 356 + 35 230 = |
Решение
| 469 + 1 843 – 1 992 = 320 | 4 578 – 2640 + 3 654 = 5 592 |
| 9 029 – 6 230 – 1 389 = 1 410 | 19 463 + 7 356 + 35 230 = 62 049 |
Задание 11
Вычислите:
| 6 036 – (1 343 + 2 876) = | 9 803 – (6 357 + 1 996) = |
| 4 378 – (2 195 – 1 880) = | 6 306 – (4 381 – 2 270) = |
Решение
| 6 036 – (1 343 + 2 876) = 1 817 | 9 803 – (6 357 + 1 996) = 1 450 |
| 4 378 – (2 195 – 1 880) = 4 063 | 6 306 – (4 381 – 2 270) = 4 195 |
Задание 12
В швейную мастерскую привезли 150 м ткани. В первую неделю было израсходовано 46 метров, а во вторую 38 метров. Сколько метров ткани осталось в мастерской?
Решение
- 1) 46 + 38 = 84 (м) ткани израсходовали за 2 недели;
- 2) 150 – 84 = 66 (м) ткани.
- Ответ: в мастерской осталось 66 метров ткани.
Задание 13
Сравните не вычисляя:
| 1 487 + 372 … 183 + 1 394 | 48 391 + (3 409 + 2 809) … (2 893 + 1 908) + 48 391 |
| 8 934 + 490 … 822 + 8 943 | 17 429 + (6 830 + 3 402) … (7 620 + 3 420) + 17 429 |
Решение
| 1 487 + 372 > 183 + 1 394 | 48 391 + (3 409 + 2 809) > (2 893 + 1 908) + 48 391 |
| 8 934 + 490 < 822 + 8 943 | 17 429 + (6 830 + 3 402) < (7 620 + 3 420) + 17 429 |
Задание 14
Решите задачу:
В овощной магазин привезли картофель и лук. Картофеля привезли 185 кг, а лука на 48 кг меньше. Сколько всего картофеля и лука привезли в магазин?
Решение
- 1) 185 – 48 = 137 (кг) лука привезли в магазин;
- 2) 185 + 137 = 322 (кг).
- Ответ: всего привезли 322 кг лука и картофеля?
Задания на тему «Сравнения натуральных чисел»
Чтобы научиться сравнивать натуральные числа, необходимо знать их порядок. Например, для сравнения чисел 568 и 425, нужно сначала посмотреть первую цифру с левой стороны, а затем вторую и третью. В данном случае, цифра 5 в числе 568 больше цифры 4 в числе 425. Поэтому число 568 больше числа 425.
Если у чисел в самой левой разрядной цифре одинаковые цифры, то сравнивают следующую цифру справа. Например, если мы сравниваем числа 823 и 815, то сначала сравниваем 8 и 8, а затем сравниваем 2 и 1. В данном случае, 2 больше 1, поэтому число 823 больше числа 815.
Чтобы сравнить два числа, которые имеют разное количество разрядов, необходимо добавить нули к меньшему числу, чтобы они стали одинаковой длины. Например, чтобы сравнить числа 76 и 542, нужно превратить число 76 в число 076. Затем мы сравниваем почередно цифры и видим, что 5 больше 0, поэтому число 542 больше числа 076.
Сравнение натуральных чисел также может быть использовано для определения отношений «больше», «меньше» и «равно». Например, чтобы ответить на вопрос, сколько яблонь больше – 56 или 89, необходимо сравнить числа 056 и 089. В данном случае, число 089 больше числа 056. То есть, 89 яблонь больше, чем 56 яблонь.
Если нужно найти разницу между количеством каких-то предметов, можно использовать сравнение натуральных чисел. Например, если у ребенка было 15 ящиков с яблоками, а потом он отдал 7 ящиков, необходимо вычислить, сколько ящиков осталось. Для этого нужно вычесть 7 из 15 и получить результат 8.
В задачах на сравнение натуральных чисел также может быть использовано умножение и деление. Например, если необходимо найти произведение двух чисел, можно использовать сравнение и умножение. Например, чтобы найти произведение чисел 5 и 7, можно составить равенство: 5 * 7 = 35. Значит, произведение чисел 5 и 7 равно 35.
Также в задачах на сравнение натуральных чисел могут быть использованы дроби. Например, чтобы решить задачу о длине отрезка, который лежит перед велосипедистом, можно использовать сравнение и деление. Например, если велосипедист проехал 375 метров за 5 минут, то его скорость можно найти, разделив 375 на 5 и получив результат 75 метров в минуту.
В задачах на сравнение натуральных чисел могут быть использованы также математические формулы. Например, чтобы решить задачу о количестве грушевых деревьев, можно использовать сравнение и квадрат. Например, если известно, что одно грушевое дерево дает 20 кг груш, а мы собрали 600 кг груш, то можно найти количество грушевых деревьев, разделив 600 на 20 и получив результат 30 грушевых деревьев.
В задачах на сравнение натуральных чисел часто используются слова «больше», «меньше», «равно». Например, чтобы решить задачу о сравнении количества яблок и груш, можно использовать сравнение и слова «больше» и «меньше». Например, если известно, что количество яблок в корзине больше количества груш в корзине, можно сказать, что яблок больше, чем груш.
Таким образом, задания на тему «Сравнения натуральных чисел» помогут развить навыки сравнения чисел, а также применение математических операций в решении задач.